Enharmonic Equivalent Notes and Scales: A Beginner-Friendly Music Theory Guide
▶️ Don't miss this Song of the Day ◀️
“Enharmonic Equivalent Notes and Scales: Key Concepts in Music Theory”
Enharmonic equivalent notes and scales are fundamental to understanding music theory. They explain why certain keys use only flats or only sharps, making it crucial for grasping the structure of Western music. Before diving into this topic, let’s quickly review the Western musical alphabet.
In Western music, the musical alphabet includes seven primary letters:
A, B, C, D, E, F, G
With the addition of accidentals (sharps and flats), this expands to twelve unique pitches, forming the foundation of Western tonal music.
This rewrite incorporates keywords like “enharmonic equivalent notes”, “scales”, “music theory basics”, and “Western music alphabet” to improve search visibility.
Twelve-Tone Equal Temperament (12-TET): A Music Theory Essential
The twelve-tone equal temperament (12-TET) system is a fundamental concept in Western music theory. It divides an octave into 12 equal parts, creating semitones with identical frequency ratios. This tuning system allows instruments to play in all keys without sounding out of tune, making it essential for genres like classical, jazz, and modern pop music.
Key Features of 12-TET:
- 12 Equal Intervals: Each semitone has the same frequency ratio of approximately 1:1.05946.
- Octave Division: Perfectly divides an octave (doubling of frequency) into 12 steps.
- Key Modulation: Facilitates smooth modulation between keys without retuning.
Traditional notation in western music theory follows the twelve tone equal temperament. These twelve pitches are as follows:
A Bb B C Db D Eb E F Gb G Ab OR A A# B C C# D D# E F F# G G#
Twelve-tone equal temperament ensures compatibility across instruments and is widely used in pianos, guitars, and many other instruments.
More Than Twelve Notes
Between these two scales, there are more than twelve distinct notes. These additional notes are referred to as enharmonic equivalents.
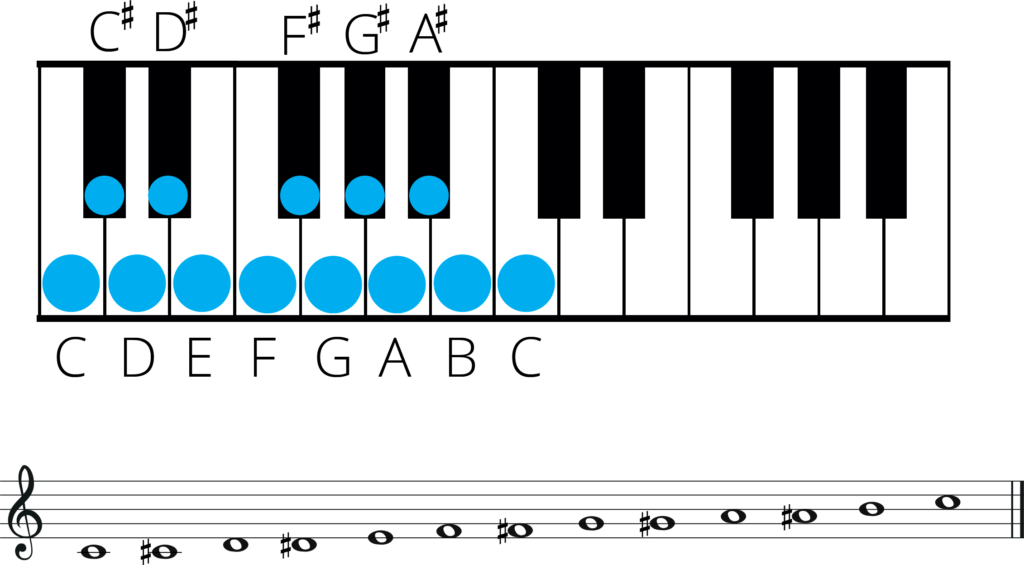
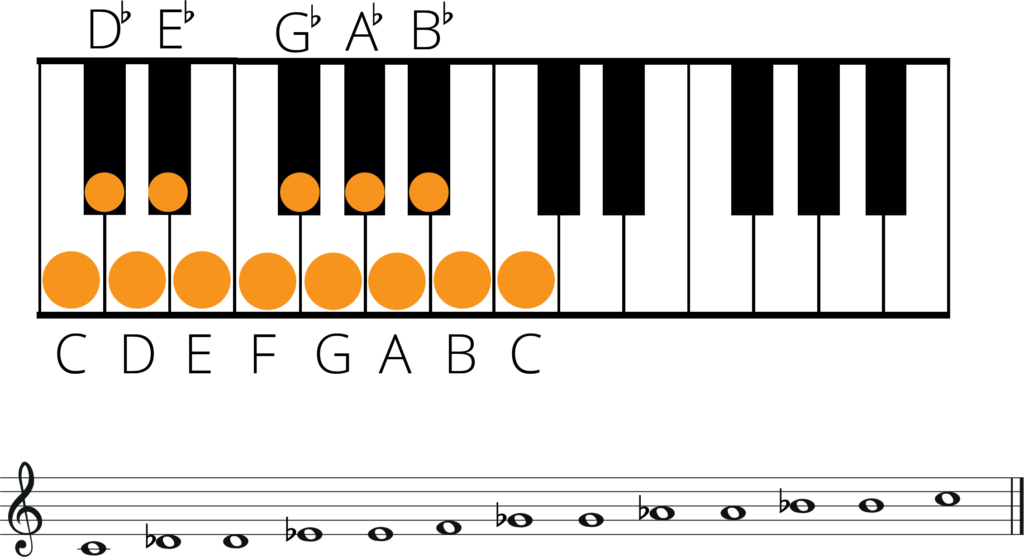
Both of the scales shown above are examples of the chromatic scale. Each of the twelve tones represents the same pitch but is written differently. These differently written notes are called enharmonic equivalent notes.
An enharmonic equivalent note is a note that has multiple names, such as C# and Db, which refer to the same pitch. Enharmonic equivalents are important for various reasons, primarily to make music notation easier for performers to read and understand.
Enharmonic Equivalent Notes
Enharmonic Equivalent Notes are notes that represent the same pitch but are written with different names. For example, C# and Db are enharmonic equivalents, as they sound the same but are notated differently depending on the musical context. These notes are essential for simplifying music notation and allowing for smoother transitions between different keys and scales.
Same Note
An enharmonic equivalent note is a pitch that has multiple names. For example, the notes G# and Ab represent the same pitch. Let’s take a look at the piano to see this in action:
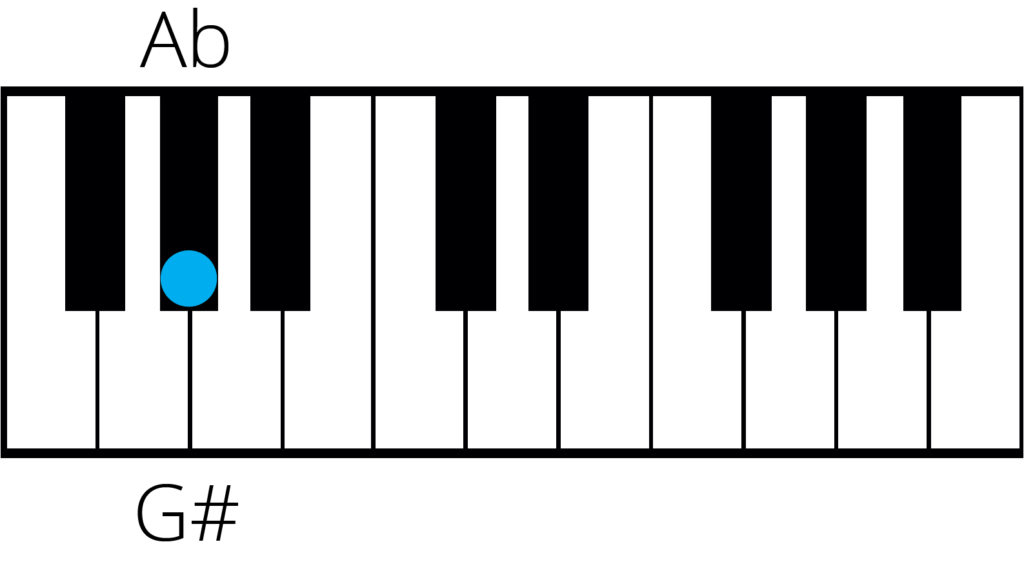
Similarly, Eb and D# are also the same note…
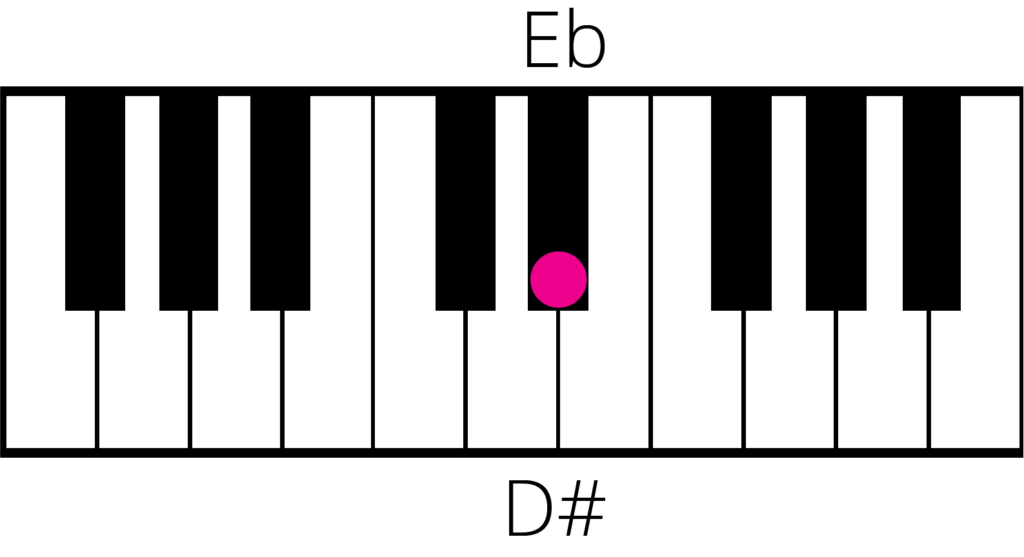
Remember a flat lowers a note by a half step and a sharp note raises a note by a half step.
We use these different note names depending on the context of particular notes in the piece of music.
If for example you are in the key of E major, this key has a keys signature of four sharps (F#, C#, G#, D#) and so it would not make sense to use E flat.

Similarly, if you are in the key of Eb major, this has a key signature of three flats (Bb, Eb and Ab) it would not make sense to use D#.

Enharmonic equivalents are useful to think about in the context of minor keys. In music theory, we have two different types of minor key. The harmonic minor and the melodic minor. In the harmonic minor we raise the seventh note and in the melodic minor, we raise the sixth and seventh note. Raising means to sharpen the note.
Let’s take the key of E harmonic minor. The seventh note of this scale is D, if we raise this note, it becomes D sharp. It would not make sense to make this D# and Eb in the context of E harmonic minor as E minor is a sharp minor. The key signature of the scale you are in is a great visual distinction when deciding what note to use.

When you compose music it is important to think about the key you are writing in to ensure you use the correct enharmonic spelling.
Enharmonic equivalents can also be double sharp or double flats.
Remember, double sharps are notes that are raised by two half steps and double flats are lowered by two half steps.
Take for example the note A double sharp. An A double sharp is in fact the enharmonic equivalent of the note B.
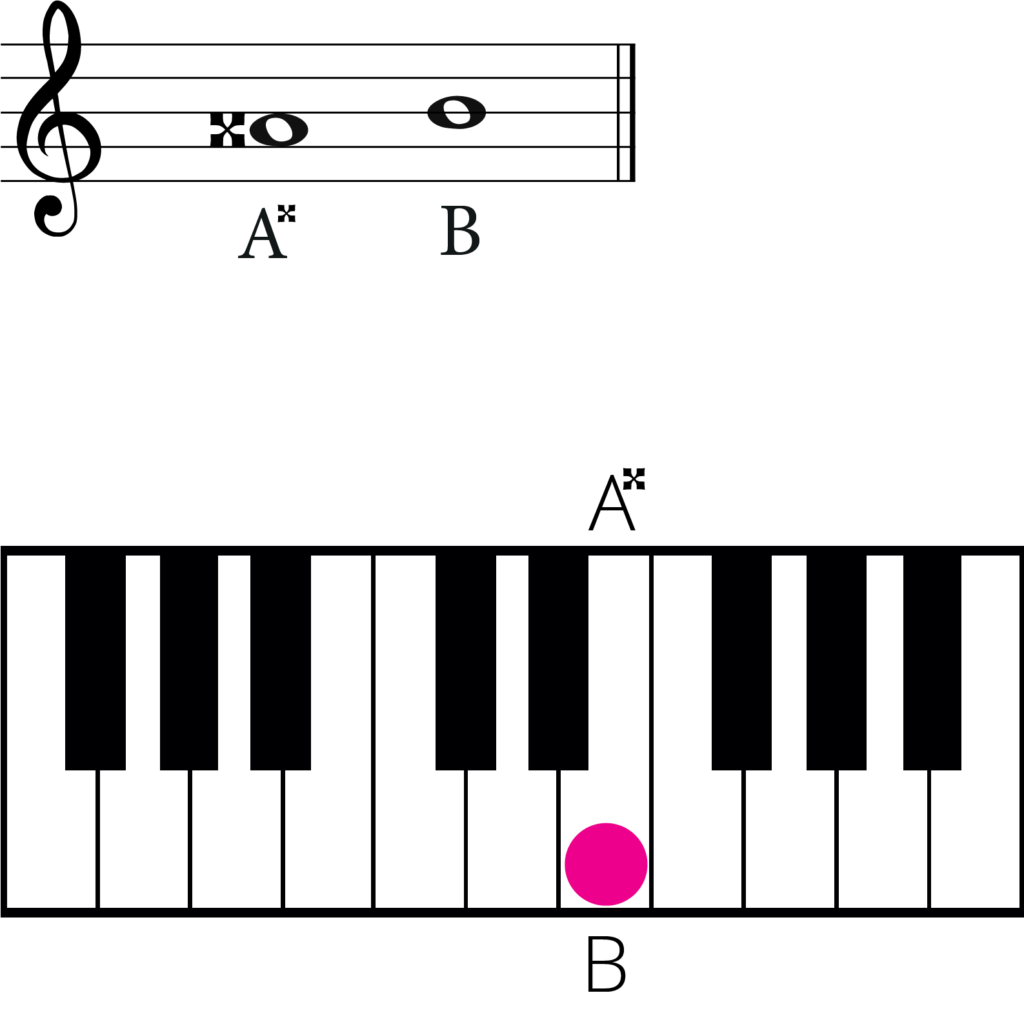
B double flat is an enharmonic equivalent of the note A.
As well as having enharmonic equivalent notes, we can also have enharmonic equivalent scales.
Enharmonic Equivalents – Scales
Enharmonic equivalent scales work in exactly the same way as enharmonic equivalent notes, in fact it is just a collection of enharmonic equivalent notes!
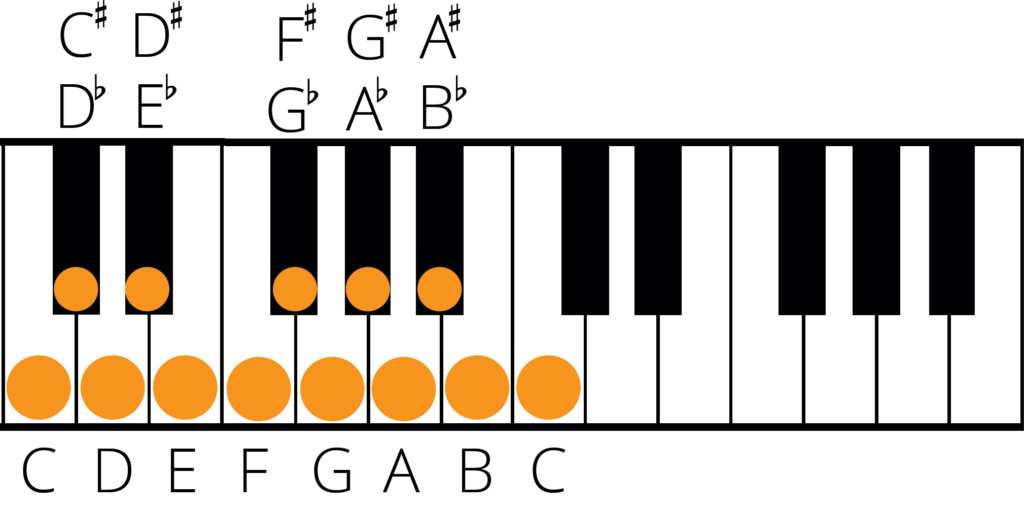
Take for example the note F#. The enharmonic equivalent of this note is Gb.
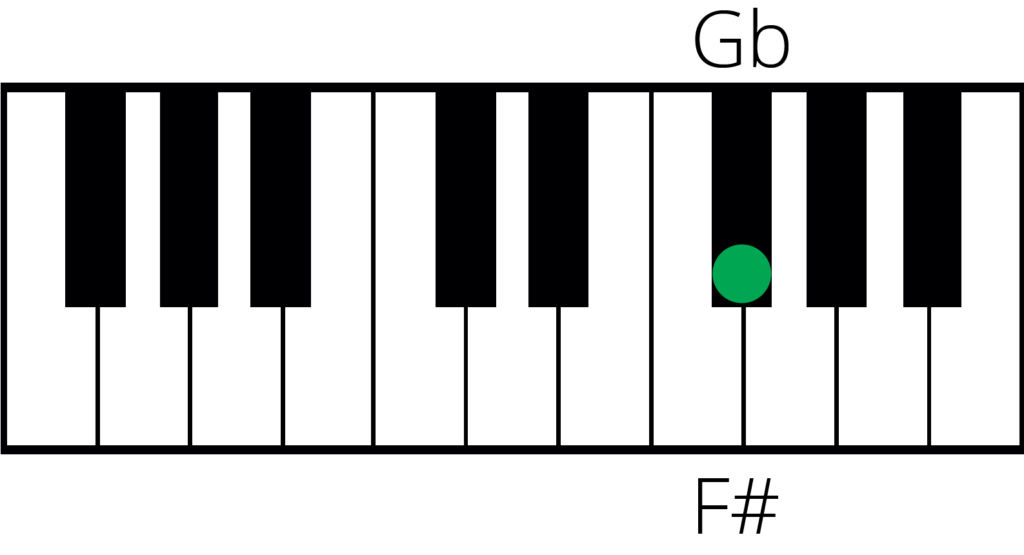
This can then be expanded into the scales.
The notes of the F# major scale are F#, G#, A#, B, C#, D#, E#, F#

The notes of the Gb major scale are Gb, Ab, Bb, Cb, Db, Eb, F, Gb

Notice how each note is an enharmonic equivalent? If you compare the two scales on the piano you can see that they are in fact exactly the same notes!
Enharmonic Equivalents – Key Signatures And Chords
As with enharmonic scales, an enharmonic equivalent key signature works in much the same way.
The F# major scale as we saw earlier has a key signature of six sharps. The enharmonic equivalent key is the Gb major scale and this key has six flats.
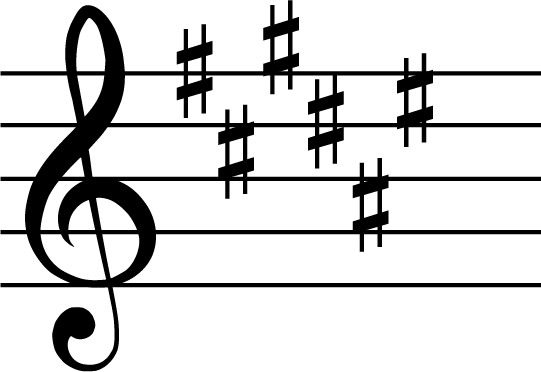

Another example would be C sharp major which has a key signature of seven sharps. The enharmonic equivalent key is D flat major and this has a key signature of five flats.

Both of these scales consist of notes that are the same exact pitch but are represented differently with alternative accidental signs. In other words, they are the same but are spelled differently.
Which scale you use depends very much on your musical passage and the key relationships. It will also depend on which key signature is nicer to read! I think you’ll agree that you would rather play in D flat major than C sharp major!
The chords within these keys follow the same rules.
The tonic chord of D flat major will sound the same as the tonic chord in C sharp major.
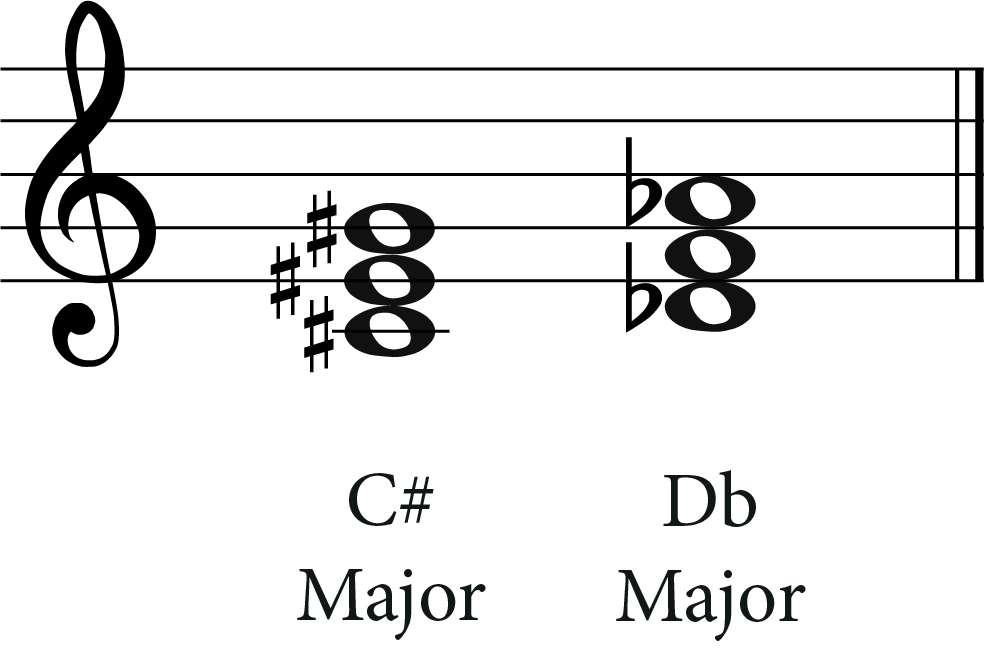
Enharmonic Equivalents – Intervals
An enharmonic intervals are slightly different to enharmonic equivalent notes but they follow the same principle.
An interval is the distance between two pitches. An enharmonic interval is two notes that are the same distance apart but spelled differently.
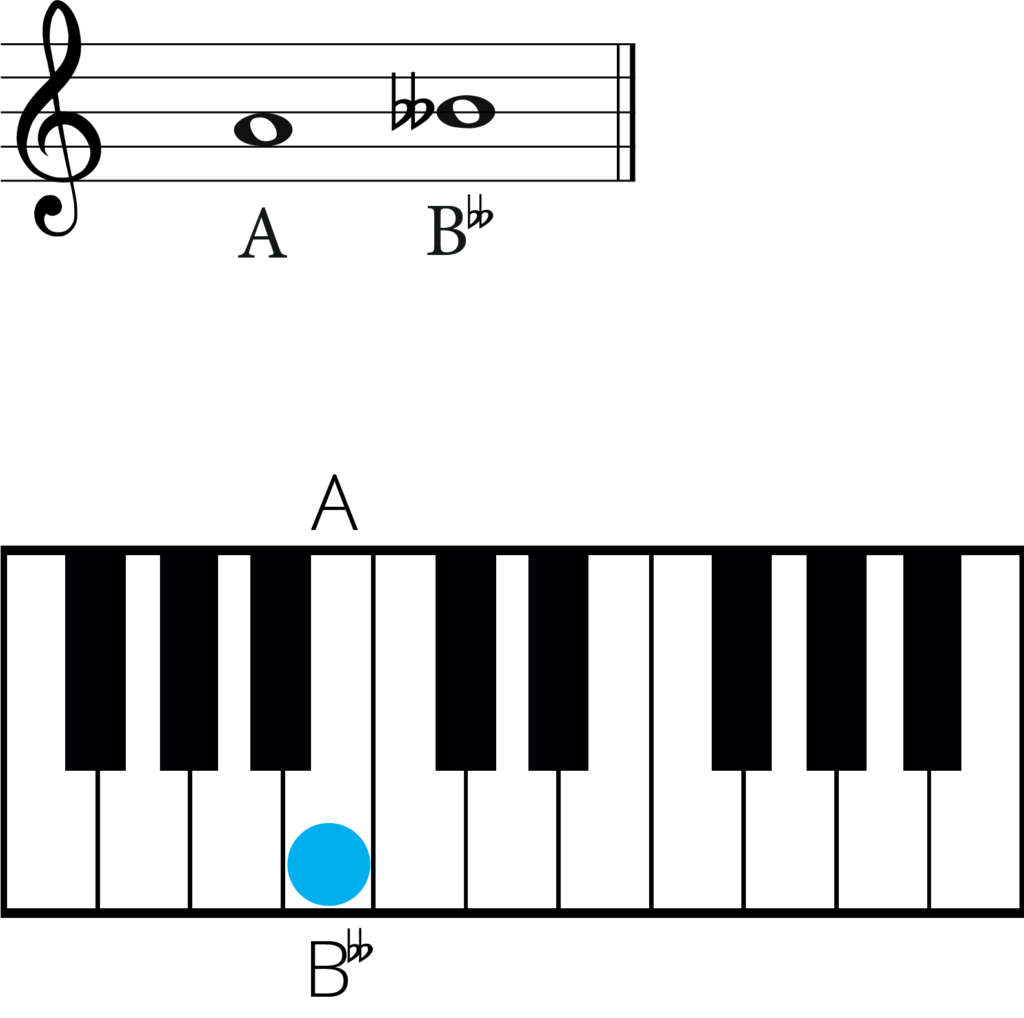
Lets look at the notes F and A. These two notes are a major third apart. The enharmonic equivalent of the note A is B double flat.
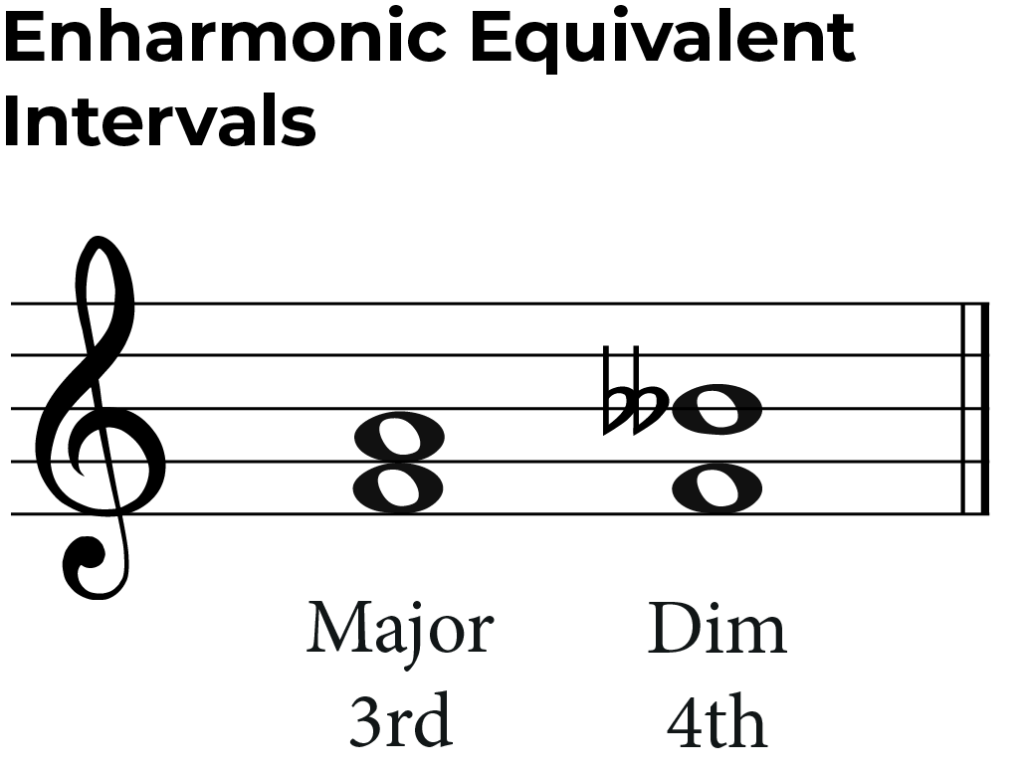
The two intervals above will sound exactly the same, but the first interval is a major third and the second interval is a diminished fourth. Learn more about this with our intervals articles.
Below you can see a chart of enharmonically equivalent notes:
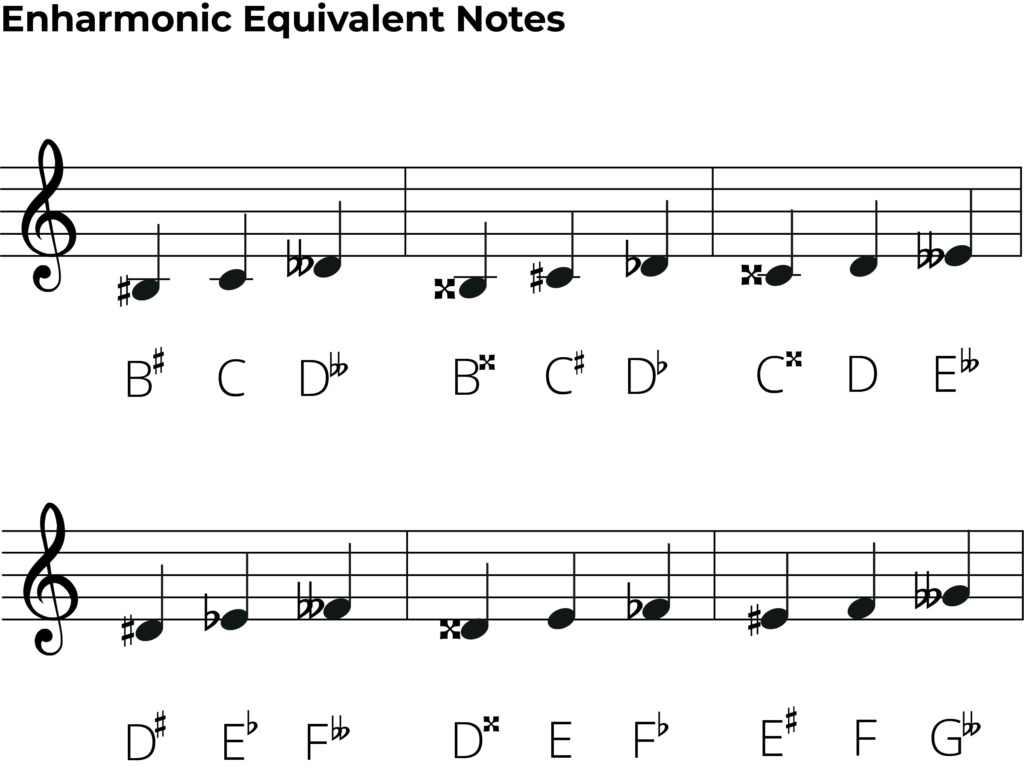

Enharmonic Equivalents Before The Romantic Period
Western music today and since the romantic period of music, we have developed a common tuning system. This is the most common tuning system you will see around today and is where the twelve tone equal temperament comes from.
Prior to this, each of these notes would have slightly different pitches and therefore would note be considered enharmonic. You can also see this within experimental musicians music where they make use of the microtonal scales. However, it is assumed that advanced musicians that play these scales are using a flexible pitch instrument such as the voice or a string instrument that is able to show these slight deviations in pitch.
How To Write The Chromatic Scale
When writing out chromatic scales in music theory, it is important to know how these are typically spelled.
In a melody ascending chromatically, you will most commonly use sharps. In a melody descending chromatically, you will most commonly use flats.

Enharmonic equivalents are very useful in music theory as they allow you more flexibility when writing music. Depending on the key of your music, you can write the same pitches but in a different way.